In a previous blog, we discussed how Rubrik has built abstractions to separate out the data layer using BlobStore, making it easy for us to manage and dedupe data in a way that is completely transparent to the application. Here, we’ll do a deep dive into a feature called Cascading Cross, which facilitates data reduction of snapshot contents.
In the early days of Rubrik, we decided to restrict cross bases crossing against each other to reduce complexity and limit the deduplication domain, in turn minimizing the impact of corruption in the data dependency chain. The downside is that this approach can lead to multiple clusters of crossed fulls with similar cross bases.
As we’ve continued to scale and build out our solution, we’ve put a lot of checks in place to detect, prevent, and fix corruptions in our system, making it imperative to allow such clusters to be crossed against each other for better dedupe. To do this, we built a feature called Cascading Cross.
Let’s take a closer look at how cascading cross works. To set the stage, this is the generic form for such topologies:
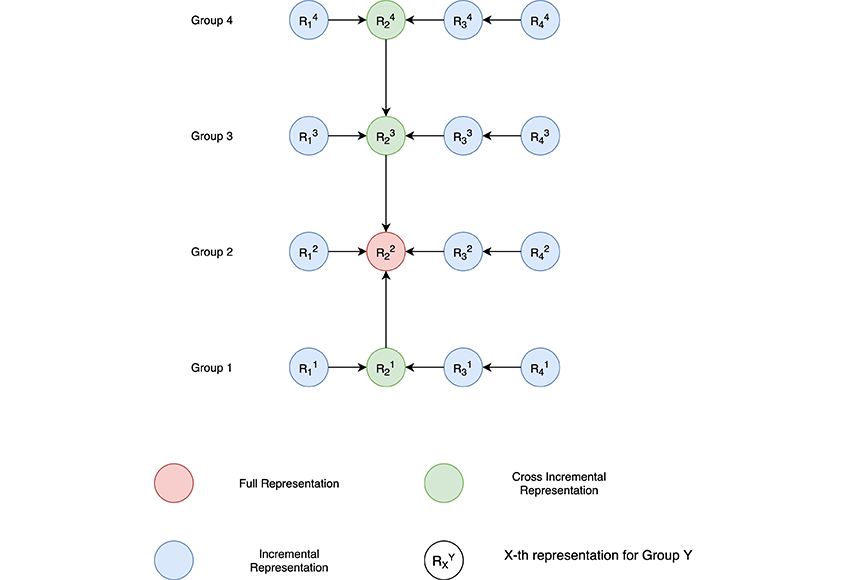
The diagram below shows that the full blobs and all cross incrementals dependent on these fulls (either directly or indirectly) produce a cross tree:
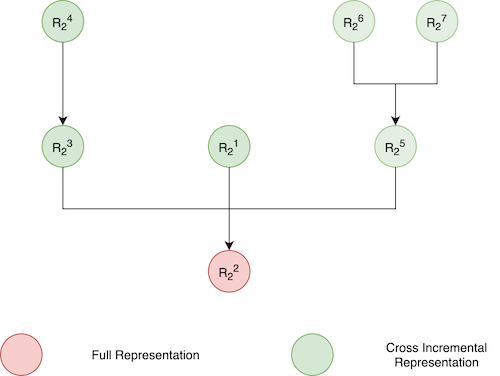
Note that as we increase the depth of this cross tree, maintenance operations like consolidation become much more complicated and inefficient. Hence, we needed to find the right height of the tree to give us maximum dedupe without compromising on the performance of other tasks. This limit plays a critical role in the algorithm for performing and maintaining the crosses.
Performing Cascading Cross
Whenever we update the dependencies in a blob chain (I elaborate on blob chains in my previous post), we perform a rebase operation that is similar to a Git rebase operation. Since, we are now also allowing cross-base full representations to participate in crossing as cross increments, we need to perform rebase across multiple groups after crossing. As an example, suppose we have following configuration:
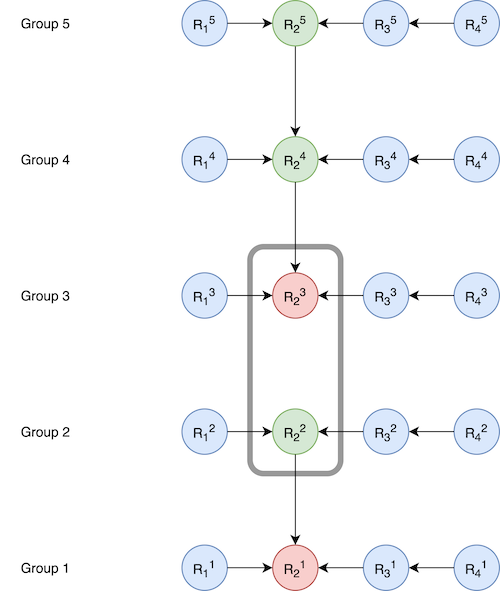
Here, R23 of group 3 is a cross base full representation and will be crossed to R22, which is a cross incremental representation. This creates a new cross incremental representation for R23 , which will not only trigger a rebase for its own group (group 3), but also for groups 4 and 5, resulting in the following configuration:
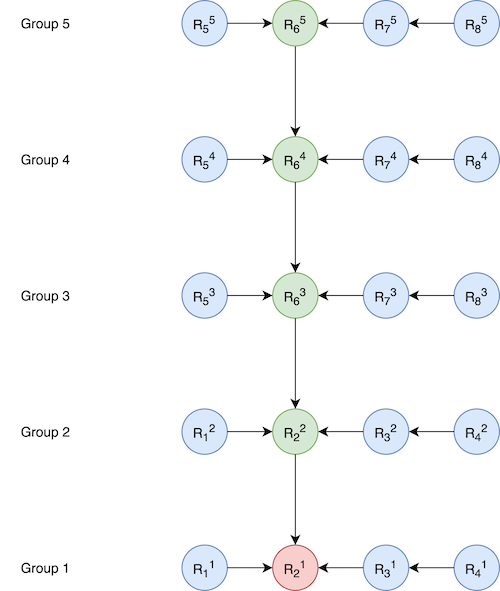
Note that we need to ensure the final height of the tree doesn’t exceed our thresholds. To do this, we store the height and depth value at each node. On every cross, updating the depth is efficient (O(maxDepth)), but in many cases, height needs to be updated on every node, making it an exponential operation. Hence, we needed a more optimal way of computing the height for every node. This problem can be mapped to the Union-Find algorithm, and we use a similar strategy in which we store a pointer and height to the last known root node on every node.
Cross Group Consolidation
As we saw above, a cross incremental may get deleted and require consolidation. This is not as trivial as normal incremental consolidation because the crosses don’t form a single chain, they form a tree. So, it is possible that multiple crosses depend on the deleted cross. If we decide to consolidate each of the dependent blobs, we may end up taking more space. Let's look into how we determine when consolidation can reclaim space.
When To Consolidate
Let’s use the following simple model to show when to perform cross group consolidation.
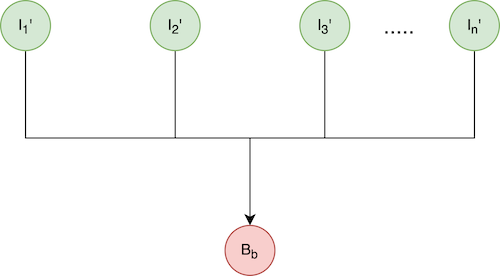
Here, In is the nth incremental blob, which can representa basic incremental or a cross incremental.
B is the base blob for all In, which has been expired and can potentially be consolidated into each of In.
Bb is the cross base of B. It could be a full or cross increment itself.
CC is B’s change rate with respect to Bb.
Ck is the change rate of Ik with respect to B.
Let’s assume that the logical size of all the blobs is L. The physical size of patch file is L*C, where C is its change rate with respect to its base. We can simply assume L = 1 in the following section, as all calculations scale linearly with respect to L.
Total physical space occupied by patch files before consolidation:
= Sum(Size(Ik ))+ Size(B)
= C1 + C2 + C3 .. Cn + Cc
= Sum(Ck) + CC
After consolidation:
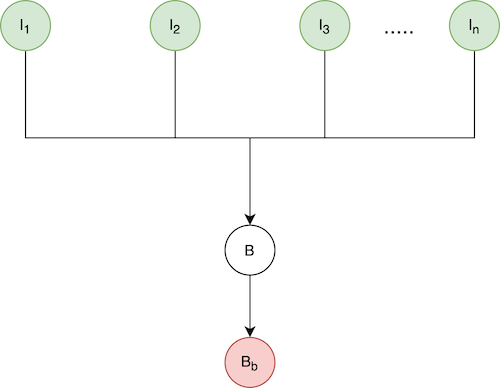
The example also shows what happens when blob(I1) is consolidated into the next blob(I2) to create I2:
Assuming uniform distribution, the total physical space occupied by patch files after consolidation
= Sum(Size(Ik’))
= Sum(Ck + CC - Ck * CC)
= Sum(Ck) + n * CC - CC*Sum(Ck)
Free space gained from consolidation
= (Sum(Ck) + CC )- ( Sum(Ck) + n * CC - CC*Sum(Ck))
= CC * (1 - Sum(1 - Ck))
We can make two observations from this:
More cross incrementals leads to less space gains. After a certain point, the space gains might actually become negative.
Higher change rates provide more space gains.
Based on this, we can compute when the space gains are large enough to pay the cost of consolidating the deleted cross.
Note that it is also possible to choose one of the Ik to replace B and have remaining incrementals depend on the chosen Ik, but we’ll keep that discussion out of scope for this blog.
Performing Consolidation
When performing a cross group consolidation, it may impact multiple groups that are dependent on the cross being consolidated. Here is an example:
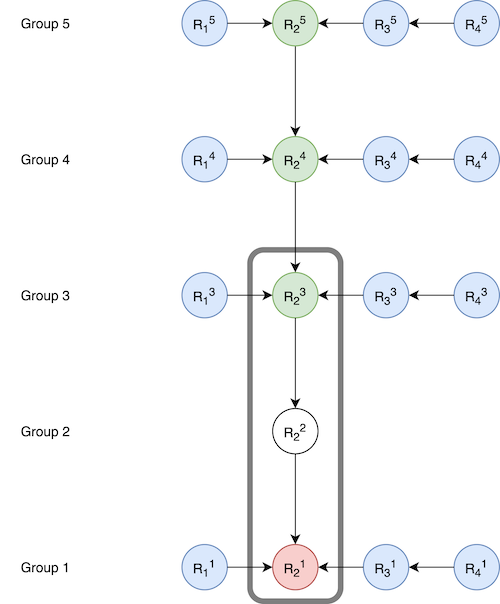
Here the chain to be consolidated is R21 <- R22 <- R23, where the head (R23) is a cross increment. This is the result after consolidation:
.png)
Note that the changes were made to Group3, Group4, and Group5. We have built an algorithm to do this multi-group rebase in an asynchronous manner for each group so that other operations don’t need to be blocked while the rebase is being performed.
Conclusion
At scale, problems which look simple at the surface can have complicated solutions and tricky challenges. At Rubrik, we make sure that we evaluate the disks and do a thorough analysis of the gains provided by the feature before implementing it.
Here we saw how Cascading Cross, which may seem as simple as enabling cross incrementals as cross bases, had a lot of caveats. We made sure to do a detailed analysis of the gains we got out of it and developed efficient algorithms and heuristics to see those gains in the field.
Want to learn more about the technology behind Rubrik? Check out these engineering blogs:
