At Rubrik, we’re big believers in data protection. But until we’re able to take consistent snapshots of our brain state and upload them to the promised hierarchical neural interconnect, we’re going to focus on backing up the more traditional machines — the ones whose smooth functioning will enable this cause.
Any complete backup solution needs a distributed, scalable, fault-tolerant file system. Rubrik’s is Atlas, which made the switch from triple mirrored encoding to a Reed Solomon encoding scheme during our Firefly release. To help you understand the motivation behind this change, this post introduces erasure coding and compares the two methods.
What is Erasure Coding?
Suppose we want to store a piece of data on a fault-tolerant and distributed file system. In this case, the loss of any single drive should not result in data loss. The only way to achieve fault tolerance is through redundancy, which refers to storing extra information about the data across different drives to allow for its complete recovery in the event of a failure. The more redundancy we add, the greater the fault tolerance.
However, the cost of redundancy is increased storage overhead. Every file system needs to make this tradeoff between availability and overhead. At Rubrik, the team chose a scheme that achieves a middle ground between the two. It works by storing redundant pieces of information in a way that allows recovery from complete storage device failures. This technique is called erasure coding.
Triple Mirroring
The first encoding scheme we used is called triple mirroring. Mirroring involves storing identical copies of each piece of data on different disks and is the simplest method of achieving redundancy. In triple mirroring, we have three copies in total, making this scheme resilient to any two failures.
And how about fault tolerance? Let’s assume for simplicity that failures are independent and that a hard drive fails with the probability 1 / 1000 on any given day (corresponding to mean time to failure of about 3 years). The probability that all three disks fail on the same day is then about one in a billion (this would be called “nine 9s” of availability in other contexts). But since we store three copies for each symbol of data, the storage overhead is expensive.
Can we devise an algorithm with similar availability guarantees but a lower storage overhead?
Towards a Smarter Encoding Scheme
In mirroring, each symbol of data is coded independently of the others. This is less space-efficient than encoding multiple data symbols together.
A more efficient method is a Reed Solomon erasure code. Suppose we want to encode two symbols: X and Y. One solution is to store X + Y as an additional symbol. The storage overhead is now 1.5x, which is twice as space-efficient as triple mirroring!
So, if we store X, Y, and X + Y, any symbol is recoverable from the other two. This method of encoding supports a single failure.
This method can be extended. Suppose for symbols X and Y, we store X + Y and X + 2 * Y. We can thus recover from two failures, but with a 2x overhead.
So, let’s get into the nitty-gritty.
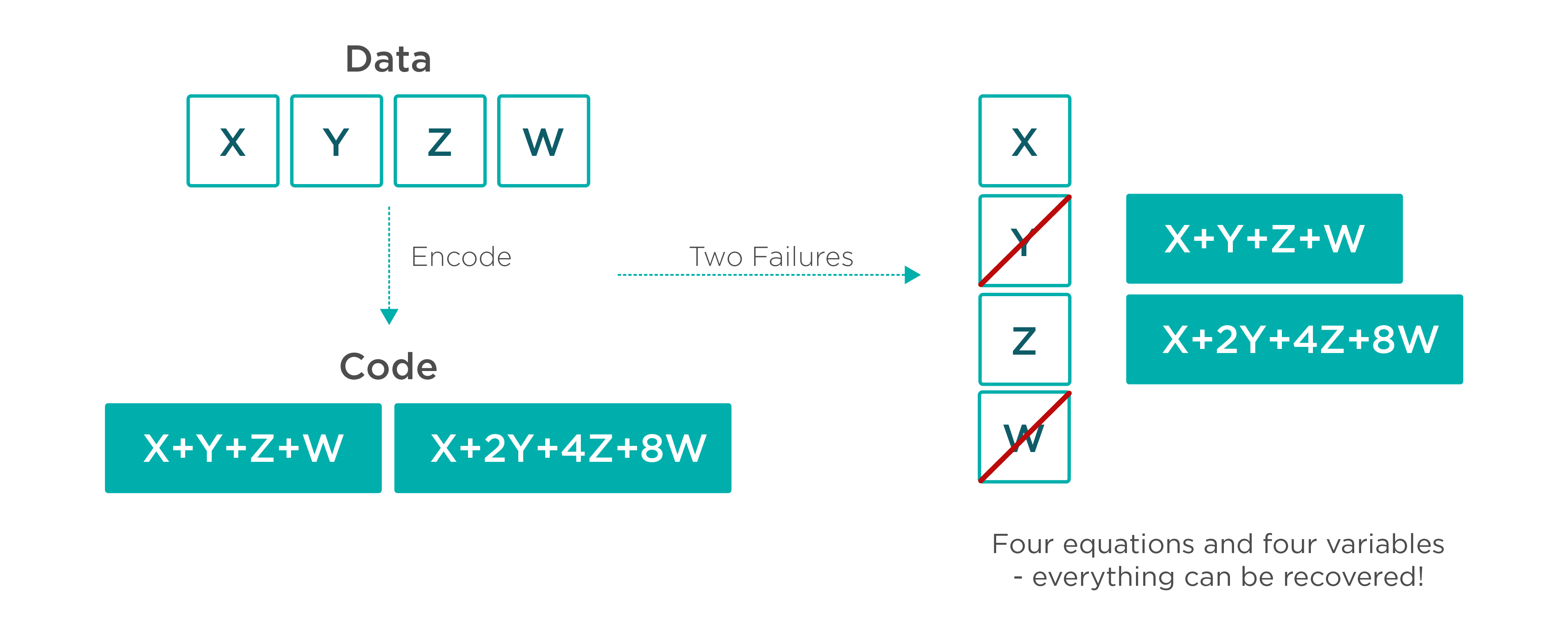
As you may see, given any M data symbols to encode, we can construct a set of N linear equations for computing additional code symbols. Suppose the equations are chosen such that any M taken together are linearly independent. If we lose any N of these symbols, we will have M equations in M variables and are guaranteed a unique solution. As a result, all the data can be recovered. A nice property of this scheme is that by default, reads are served from the data symbols, so we do not pay the reconstruction overhead if there are no failures (as is the common case).
The above describes Reed Solomon erasure codes. The part I’m not going into is that these computations are not performed using real numbers, but over a mathematical structure called a Galois field. This allows us to use the same word size for data/code symbols, as well as known constructions for the systems of linear equations.
Reed Solomon encoding with 2 code blocks for every 4 data blocks delivers a scheme that is tolerant to two failures and has an encoding overhead of only 1.5x. As a result, we have a similar level of fault tolerance as triple mirrored encoding but with twice the capacity! The Atlas file system is built to make intelligent tradeoffs between overhead and availability, depending on the performance and durability requirements of the data stored on it.
Want to learn more? Read our engineering blog: Introducing Atlas, Rubrik’s Cloud-Scale File System.
You can also watch our Tech Field Day 12 presentation on the technical details of Atlas.
TL;DR

