Simulating Filesystem Tree with Billions of Files: Part 2

The problem and constraints

Following up on our Simulating Filesystem Tree with Billions of Files series, let's imagine that we want to create a filesystem with 1 billion inodes in memory. At this scale, every single byte used to represent the inode will use 1GB of memory. Just with the inode numbers, each with 8 bytes, will use at least 8GB of memory. 

If we consider, conservatively, that each inode will use approximately 50 bytes of space, it will not be feasible to store this information in memory. We also don’t want to put this data on disk and read it because that will slow down the throughput.

This constraint means that we must be able to generate a part of the filesystem tree(or a subtree) as and when needed. With that in mind, we built on the idea of simulatables.

Simulatable

VFSim is built of many small independent building blocks: Simulatables. A “simulatable” can be defined as an object that has an initial state and allows mutations to be applied on it. This gives us the ability to build any simulation capabilities for small objects and compose them to have very complex simulatable objects. 

This simple but effective construct can help us implement snapshotting capabilities for very complex objects whose sub-objects are themselves simulatables, giving us the ability to go back in time and verify things that the simulator has created earlier. This will help us solve our problem to generate the same subtree every time for a given filesystem configuration.

The Filesystem Tree

VFSim is created by a simulatable building block called InodeSimulatable. InodeSimulatable simulates a given Inode in a large filesystem tree. An Inode could represent any of the following:

1. Directory
2. File
3. Symbolic link to a file
4. Hardlink

Internally, InodeSimulatable has two simultables–Metadata Simulatable and Data Simulatable–both of which modify part of the Inode state. The metadata simulatable generates the following state for every inode:

• Inode-number - unique 64 bit integer for each inode
• Name
• Parent-path 
• InodeType - file/directory/symlink
• Sub-tree-size (or just file-size if InodeType is file)
• Access-time, change-time, create-time and modified-time
• Pointers to child Inodes

The data simulatable does the following for every inode that is a file:

• Generate data for the file and enable overwrites, inserts and deletes with snapshots.

Algorithm to generate filesystem tree

All the random number generators used in the algorithms are pseudo-random, so they always generate the same distribution for the given seed. We take the seed as part of the configuration file to initialize the simulator  and each mutation is of the form (bytesAdded, bytesDeleted).

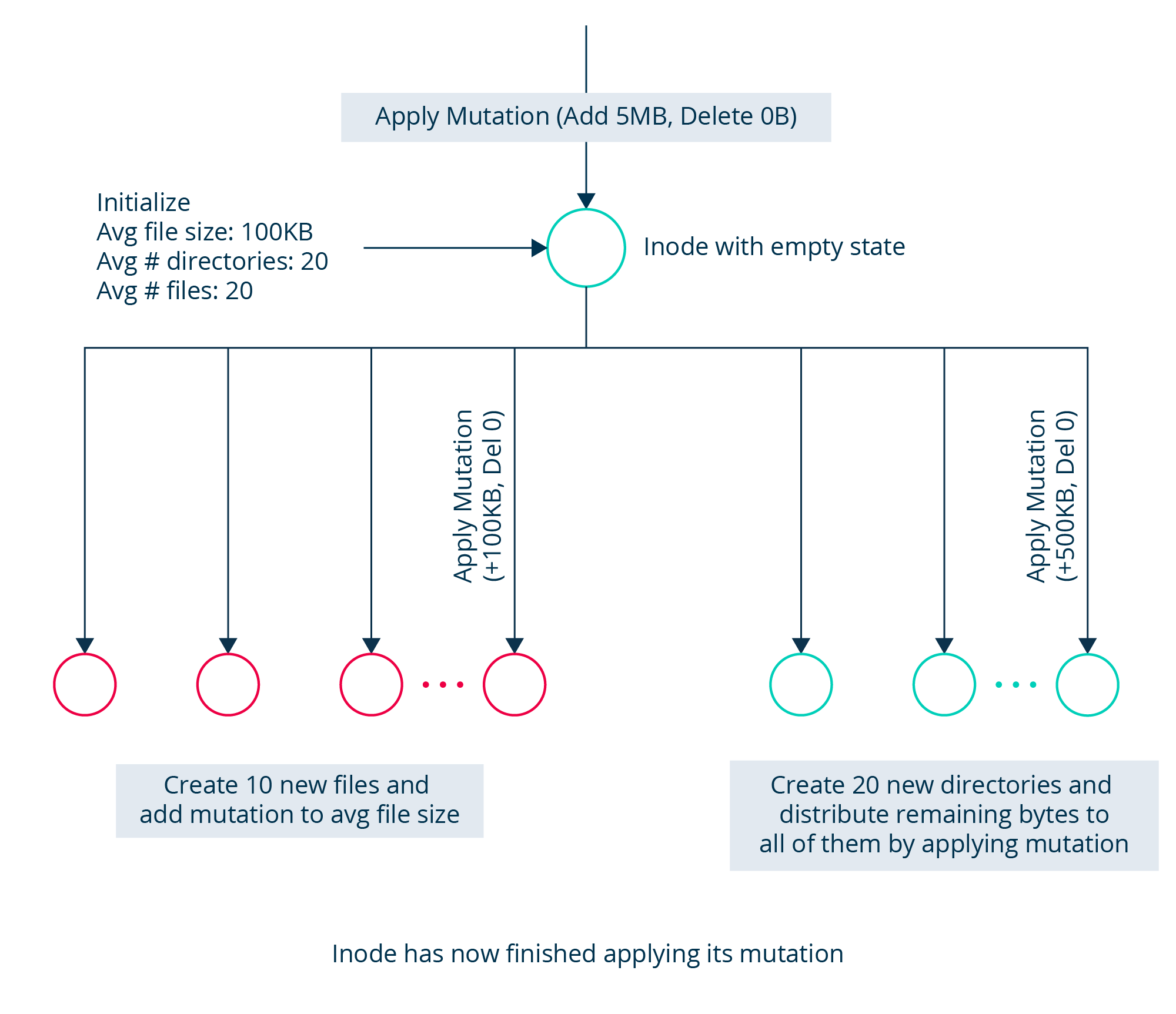
The algorithm for applying a mutation for Inode (at generation 0) goes as follows:

1. For Generation 0, we will always have bytesDeleted to be 0.
2. Create files and distribute bytes for each file based on the average  file size parameter.
   1. During the generation we modify the state of each file by adding mutations to the newly created file. Each mutation will look like Mutation(bytesToAdd, 0). bytesToAdd will be taken from the mean file size for a given distribution, for example if the average file size is say 100MB, and we want an exponential distribution of file sizes in the filesystem, we draw a random number from exponential distribution whose mean is 100MB and send that as mutation to the file inode.
3. Create directories to distribute the remaining mutations to the child directories
   1. Create empty directory Inodes based on the directory fanout distribution. For example, similar to above if directory fanout(average number of directories per directory) is 20, we randomly draw a number from uniform distribution whose mean is 20.
   2. Apply Mutations to each of them uniformly to distribute all the remaining bytes.
   3. Note that while applying these mutations we might not be able to satisfy all the constraints - file fanout, directory fanout, file size, and distribute all the bytes. We try to do the ensuring that all bytes are distributed to the children. In the end, we can be sure that the sum of all bytes belonging to the child nodes in the subtree is equal to the sum of all mutations applied to the root.

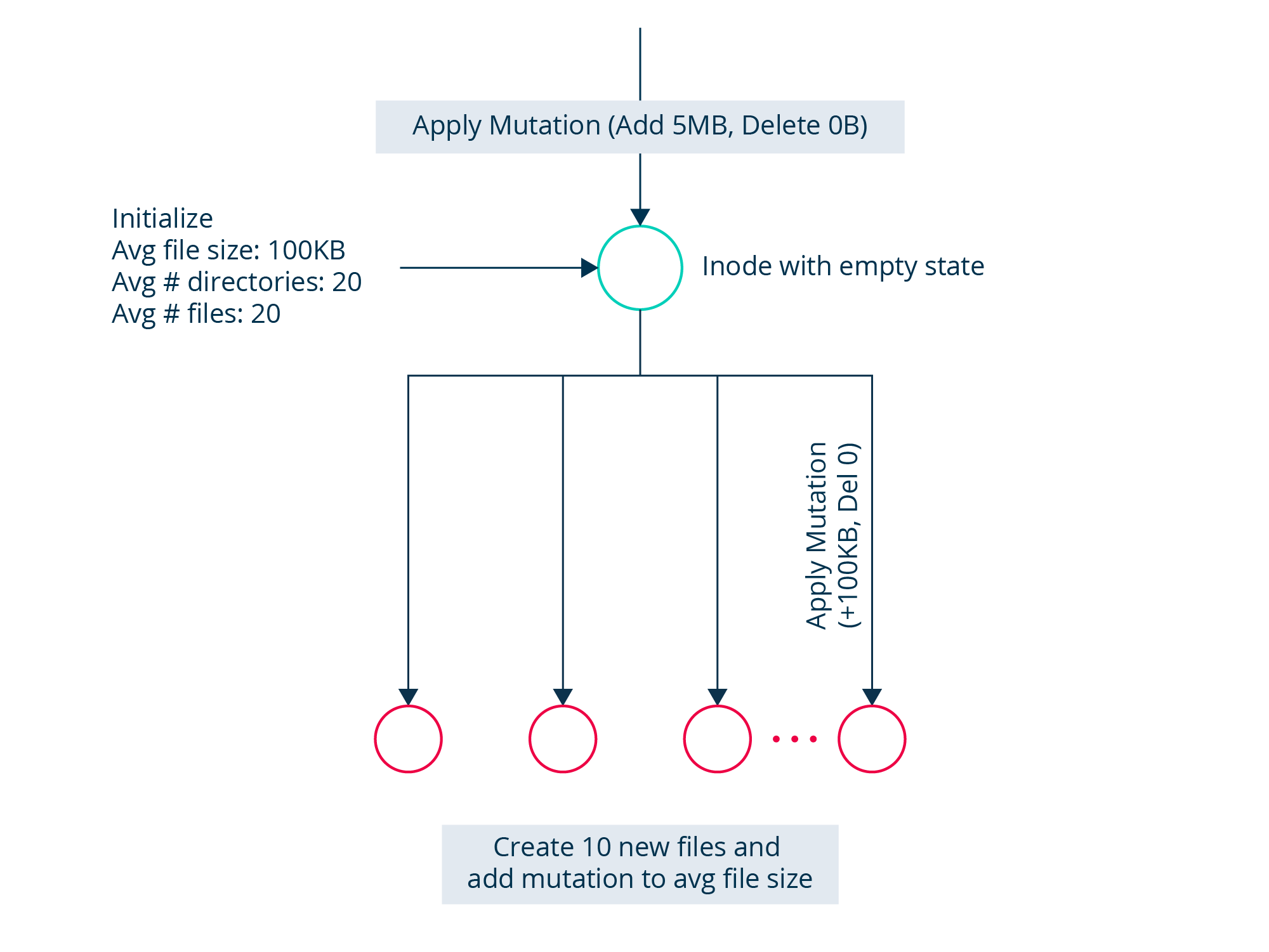
This illustrates the algorithm of simulation on the root inode for first generation, it depicts the distribution of all the bytes at a given inode.

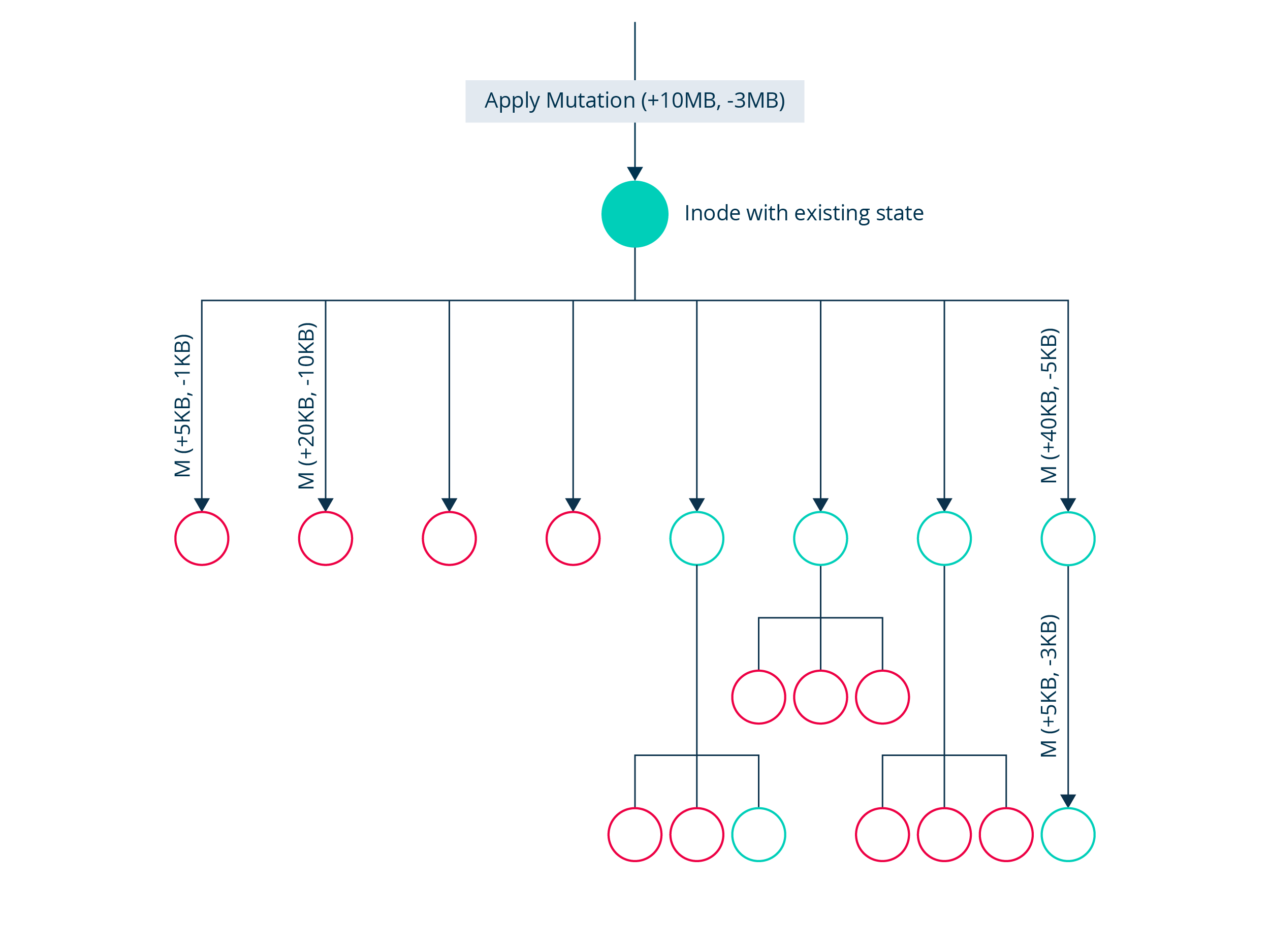
For an inode with an existing state (includes child inodes with files and other directories), the algorithm for applying the mutation goes as follows:

1. We can have non-empty bytes to be deleted as part of mutation i.e. mutation could now be (Add 100MB, Delete 20MB). This mutation would add net 80MB, but could result in deleting some files to compensate for 20MB deletion, adding more files or changing data in the existing files for adding that 80MB.
2. Distribute bytes to existing files and directories:
   1. First satisfy delete bytes:
      1. Put a portion of them to fully delete files check files, for example if total bytes to delete is 100MB and 20% of it is set to delete all files, then we can fully remove inodes which size is less than 20MB.
      2. After that, distribute the remaining mutations as bytesDeleted to the children.
   2. Distribute bytes to add:
      1. Put a portion of the bytes to add to create new inodes and recreate them.
      2. Distribute the remaining bytes to all inodes in the directory.
   3. Club (a) and (b) for each inodes that are not deleted and send as single mutation of the form (bytesAdded, bytesDeleted)
3. Note that this can also lead to deletion of entire files/directories from the node, when all the bytes of that child is removed as part of mutation distribution.

One thing to note is, the entire algorithm described above applies mutations down the filesystem tree, essentially generating the whole filesystem tree from the root and not just a specific subtree and this won’t still fit in memory. However, to be able to fit the entire generation in memory and to go back in time, all we need to do is to lazily apply a mutation by taking the following steps.

First, store the incoming mutations and lazily apply them when needed. This allows for each node to have all the mutations that should be applied stored in it. Then it can apply whenever it wants to, and get the state. This makes us to generate those parts of tree which is required

Second, if at any point of time we are going over a threshold number of nodes, we reset the state of the node - which un-applies all mutations and make it an empty node. This means that if we unapply all mutations at the root node, we will again begin with the empty inode with no children, thereby pruning all the nodes below it and an empty tree. Because the mutations applied previously are stored in order of arrival, we can always re-apply them when needed. To generate the same random numbers again, we store the “seed” of each inode which remains the same across generations.